消費者物価指数のニュースから、リタイア後を想像する。

リタイア前に遭遇する、生まれて初めての物価上昇

最近物価が上がってきたなということを実感します。
時計や車のように、余り興味が無い物の値段が上がっているのであれば、私には関係ないと思えるんですが、生活に必要不可欠な物の値段が上がっているところが困ったところです。

高い高いと思っていたら案の上で、12月の消費者物価指数は4%も増えたようです。
16カ月連続の上昇も嫌な感じですが、それより気になったのが1981年12月以来、41年ぶりの伸び率という部分です。
生まれる前やんけ・・・

エラー

nordot.app

私は家計簿を毎日つけているので、つけていない人に比べると価格の上昇には敏感です。
直近3カ月の食費の推移を見てみると、2022年10月が22,096円、2022年11月が23,175円、2022年12月28,328円と徐々に上昇していることが分かります。

新居に移ってきてから、外食が減ったので以前に比べると食費自体は下がっていますが、自炊していても食費は増加傾向にあります。

これからリタイアしようと言うのに、4%の物価上昇とか勘弁して欲しいものです。

インフレ率の恐怖を疑似体験する。

12月の物価上昇は4%でしたが、ふと思いました。
このままこの物価上昇が続くとリタイアはどうなるのかと。

毎度おなじみの逃げ切り計算機を使ってシミュレーションしてみようと思います。
比較しやすいように、リタイア年齢、支出、年金、貯蓄額、年間利息は同じでインフレ率だ変えて試してみます。

逃げ切り計算機の入力条件は、以前試した場合と同じ条件にしようと思いましたが、逃げ切り計算機がアップデートされていました。
なぜかクリスマスに・・作者もよりによってクリスマスに逃げ切り計算機のアップデートしなくても良いのにと思いましたが、より実態に近くなったのでナイス改修です。

変更点は、以前は「受給年金のインフレ連動(あり/なし)」だけでしたが、年金のマクロ経済スライド方式を取ると、インフレ率に連動しないので、「受給年金の年間インフレ率」に変更したようです。

年金受給額のインフレ連動はしないで設定したいので、受給年金の年間インフレ率は0%にしておこうと思います。

現在の年齢・・・50歳
年間利息・・・4.0%
年間支出額・・・240万円で固定（月20万円）
年金受給開始年齢・・・70歳
受給年金の月額・・・10万円
物価の年間インフレ率・・・1.0％と4.0%で比較
受給年金の年間インフレ率・・・0%

結果は以下のようになります。

これは以前にも試しましたが、ちょうど平均寿命くらいまで資産が持つ資産と支出の条件です。
この結果で推移すれば、男性の平均寿命は 81.47歳、女性の平均寿命は87.57歳の平均寿命までは資産が持つ計算になります。

インフレ率が4%になった場合はどうなるのでしょう。

想像はできましたが、思ったより強烈でした。
86歳→70歳まで16年分も資産寿命が短くなるという結果になりました。
年金受給直後に一文無しの状況になり、年金は120万円なのに、生活に必要な最低限の支出は500万円以上という、物価上昇の恐ろしさを味わうことができます。

インフレは怖いが、続きはしないだろうと思っている訳

こういったシミュレーションをすると、リタイアに不安を感じる人も多いでしょう。
ですが、私は左程心配していません。

なぜなら、インフレが進むと投資利益もまた増えるからです。
資産の評価額もインフレ率と連動して増えるので耐えられるでしょう。
上のシミュレーションでは年間利息を4.0%で設定していますが、実際インフレが進んでいる状況であれば年間利息も4.0%以上になっているだろうということです。

もう1つ理由があります。
それは、日本は高齢者が政治家を決めているからです。
年金生活者から見ると物価上昇は、支出が増えるだけの害悪でしかありません。
年金生活者からすれば、デフレの方が望ましいんです。
貯金が増えたのと同じですからね。
デフレが続いたのも、ある意味政治が機能しているからでしょう。

そんな有権者の過半数の高齢者は、年金の支給額はそう増えないのに、インフレ率だけが上昇して生活の質が下がり続けるような状況を許さないでしょう。

そうなればインフレに対応する政治家が自ずと選ばれることになりますので、今のインフレ率がこのまま続くということはまず無いでしょう。

とは言え、まだ対応できていませんね。
2023年度の公的年金額は、インフレ率に勝てず0.6％の目減りだったようです。

エラー

nordot.app

ただ、この状況のままと言うことはまずありえません。
高齢者からすると生活がかかっている訳ですから、死に物狂いでインフレ対策してくれる政治家に投票するでしょう。

ちなみに年金が0.6%の目減りする条件で逃げ切り計算機を使って計算すると、以下のような結果になります。

年金の受給直後に資産が無くなるので、結果は70歳で同じですが受け取れる年金額は異なります。
年金は234万円になっており、多少資産寿命が伸びる結果になります。

年金受給後の状況を観察したいので、貯蓄額を2,000万円ほど追加してみると、結果はさらに顕著になります。

受給年金のインフレ率の有り無しで、81歳から85歳と4年分資産寿命が伸びました。

私が想像していたより、資産寿命は伸びませんでした。
それもそのはず年金の増加よりも、支出の伸びがえぐいです。
今の240万円の支出が82歳時点で809万円、86歳時点で947万円になっています。

こうなると、いわゆる普通の生活をしている人は年間支出が1,000万円以上になるということになります。

日本で年1,000万円以上の支出が当たり前になるところなんて今は想像できません。
実際、日銀の情報で確認する限り、40年前の1983年の消費者物価は2020年を100とした場合、80.3です。

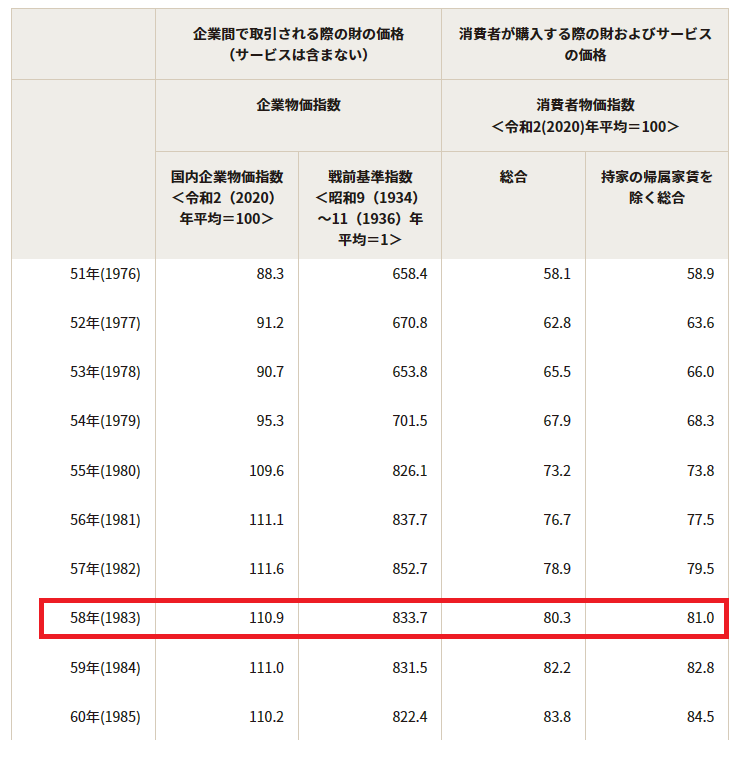
40年で、大体20%程度の上昇に留まっているということです。

総務省の2021年の家計調査では、単身世帯の平均支出は月に155,046円です。
年間だと1,860,552円、約190万円です。
これが今後40年で、20%程度増えると考えても、228万円です。
現在の逃げ切り計算機のシミュレーションどおり、年間240万円の支出で考えてインフレ率0%で計算してもお釣りがきます。

40年後もこれまでと同じということは無いでしょうが、これから経済規模が縮小していく日本で、人口ボーナス期の日本と同じように経済拡大していくことは無いでしょう。

経済規模が拡大して需要が増えるからインフレになるのであって、経済規模が縮小する国でインフレは起き辛いでしょう。
このことからも4%のインフレ率が、このあと数十年に渡って続くなんてことは無いだろうなと思っています。

悪性のインフレはありそうですけどね。ハイパーインフレとか・・
そうなったら家のローンをお菓子買う感覚で返した後、また考えようと思います。